All students should graduate from high school ready for college, careers, and citizenship.

1. Understanding
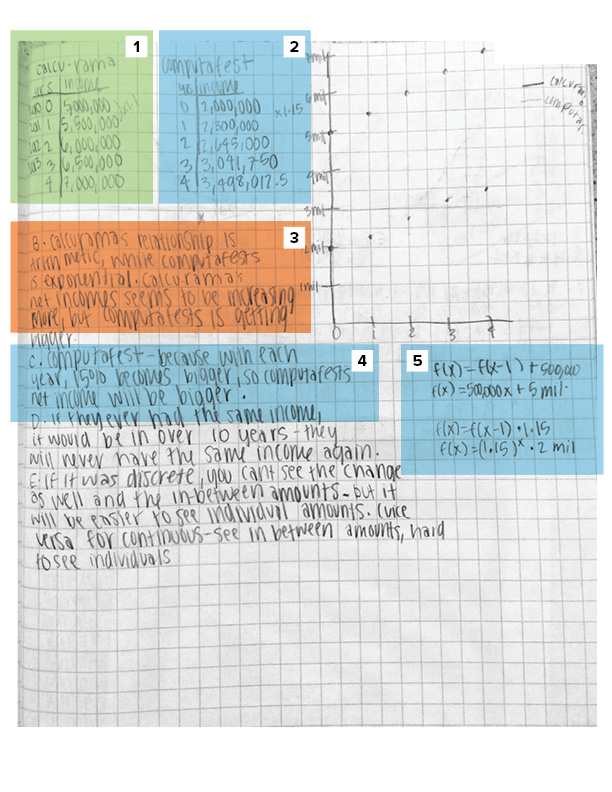
What is the student looking at when the student multiplies by 1.1? Is this an attempt to see if the table could be described with a common factor?
2. CCSS Alignment
The student correctly identifies parameters for both linear and exponential functions, is capable of using large numbers, and is handling the percent growth correctly in both equations and tables.
Standard referenced:
HSF-LE.B.5: Interpret the parameters in a linear or exponential function in terms of a context.
3. Comprehension & Application
SMP.7: Look for and make use of structure.
The student understands the structure of the two function types. The student makes a claim about the functions that is not supported by the tables or graph, but seems likely to have come from understanding the structure of the types of functions.
4. CCSS Alignment
The student recognizes that the exponential equation will overtake the linear one. The student states that initially, the linear increases faster, eventually the exponential increases faster.
Standard referenced:
HSF-LE.A.3: Observe using graphs and tables that a quantity increasing exponentially eventually exceeds a quantity increasing linearly, quadratically, or (more generally) as a polynomial function.
5. CCSS Alignment
The student can create linear and exponential functions correctly.
Standard referenced:
HSF-LE.A.2: Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
