All students should graduate from high school ready for college, careers, and citizenship.

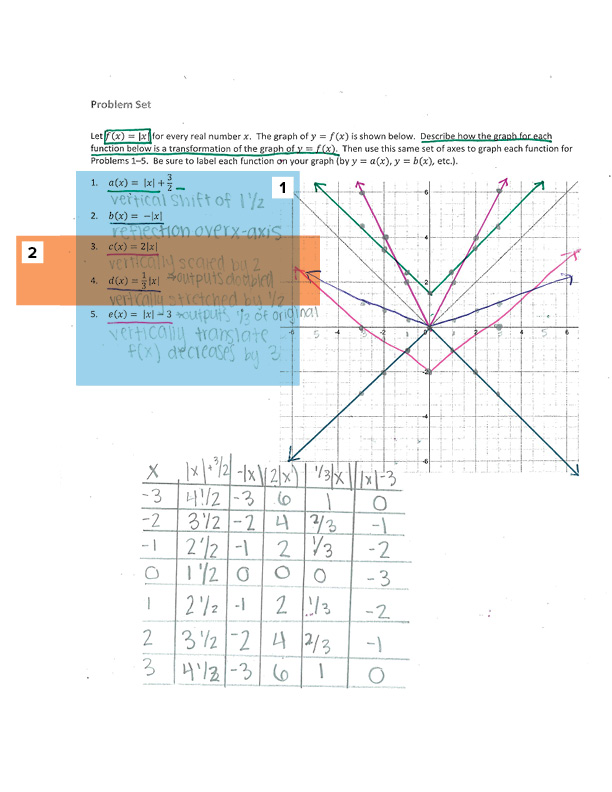
1. CCSS Alignment
In identification of the effect of the values of k on the graph, the student used both distance and direction in their descriptions of the transformations as expected in standard HSF-BF.B.3.
Standard referenced:
HSF-BF.B.3: Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k (both positive and negative); find the value of k given the graphs. Experiment with cases and illustrate an explanation of the effects on the graph using technology. Include recognizing even and odd functions from their graphs and algebraic expressions for them.
2. Comprehension & Application
SMP.6: Attend to precision.
In the descriptions for #3 and #4, the student uses “vertically scaled” and “vertically stretched,” respectively. However, in #4, the “stretch” is first described as “by 1/2” and described as changing ”by 1/3.”
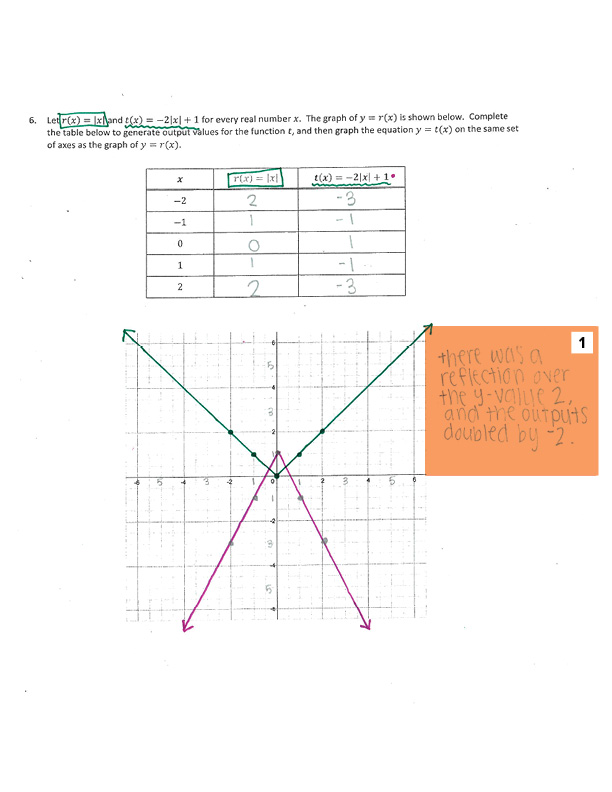
1. Comprehension & Application
SMP.6: Attend to precision.
The language used here is not precise and shows a lack of understanding in the description of “reflection over the y-value 2.” In addition, the use of, “the outputs doubled by -2” is also not precise or clear.
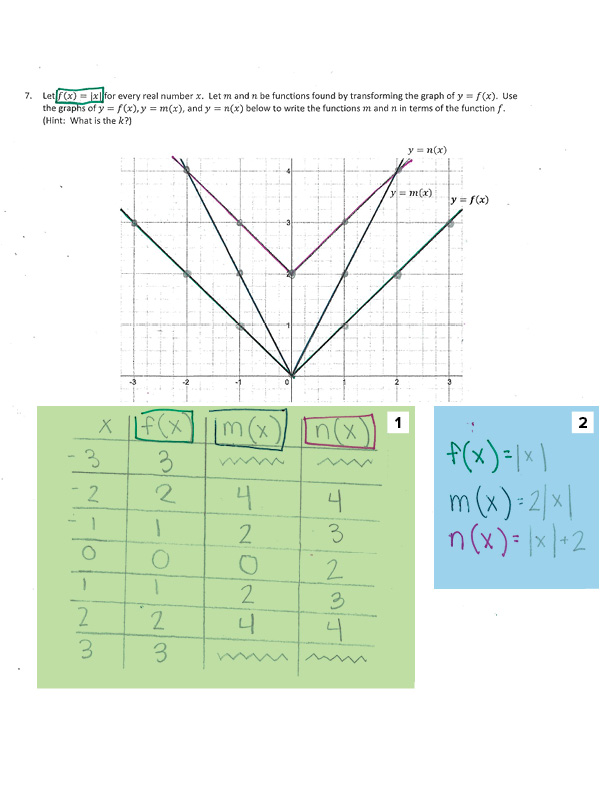
1. Understanding
While the student was able to generate equations with the correct values for k, the student also attended to the intermediate step of creating tables. It is unknown whether the table was created during the process of graphing or as justification.
2. CCSS Alignment
The student proficiently wrote the functions m and n in terms of the function f.
Standard referenced:
HSF-BF.B.3: Identify the effect on the graph of replacing f(x) by f(x) + k, k f(x), f(kx), and f(x + k) for specific values of k (both positive and negative); find the value of k given the graphs. Experiment with cases and illustrate an explanation of the effects on the graph using technology. Include recognizing even and odd functions from their graphs and algebraic expressions for them.
