All students should graduate from high school ready for college, careers, and citizenship.

1. CCSS Alignment
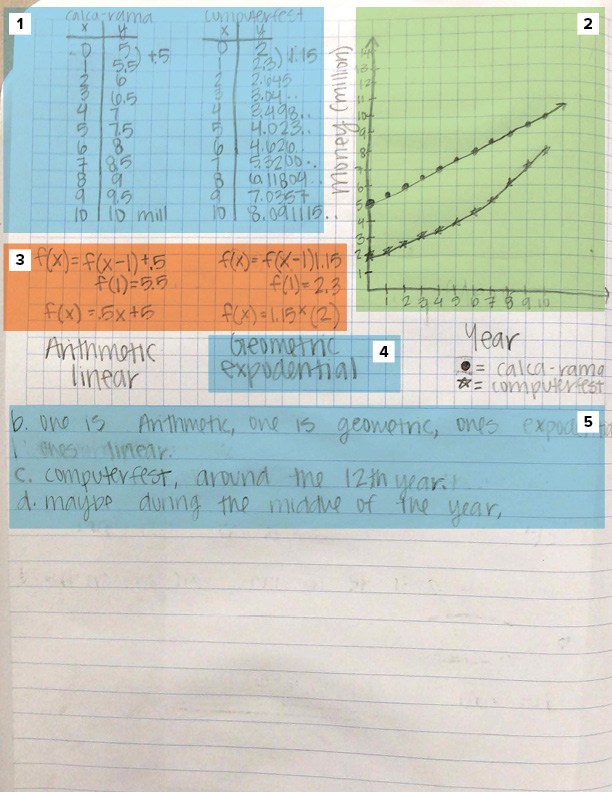
The student is clearly using the graph and the table to recognize that the exponential function continues to change at an increasing rate and will overtake the linear function at approximately 12 years.
Standard referenced:
HSF-LE.A.3: Observe using graphs and tables that a quantity increasing exponentially eventually exceeds a quantity increasing linearly, quadratically, or (more generally) as a polynomial function.
2. Understanding
There is evidence of good reasoning that shows up in the student’s graph. Without extending the student’s table or graph, the student can reason where the intersection point occurs by the student’s understanding of exponential growth.
3. Comprehension & Application
SMP.7: Look for and make use of structure.
Compare the structure of the explicit linear and exponential equations with the corresponding recursive functions. We are wondering why f(1) is used as the starting amount parameter in the recursive rules, but f(0) is used as the corresponding parameter in the explicit rules. Does the student not see these as corresponding parameters, and the same value can be used for each rule?
4. CCSS Alignment
The student correctly uses the parameters for both the linear and exponential functions and recognizes that the percent growth rate is exponential.
Standard referenced:
HSF-LE.B.5: Interpret the parameters in a linear or exponential function in terms of a context.
5. CCSS Alignment
The student recognizes the relationship between linear and exponential functions.
Standard referenced:
HSF-LE.A.2: Construct linear and exponential functions, including arithmetic and geometric sequences, given a graph, a description of a relationship, or two input-output pairs (include reading these from a table).
